Computation of the g-forces involves a calculation based on the speed and the radius of curvature of the path. To determine the gentlest possible turns we used Geogebra, which is a free, open source, geometry software tool. We devised a geometrical construction such that given an approach line, a turn-off point on the line, a way point (labeled North Citgo in the diagrams), a target point, and duration for the roll maneuver, we could produce left and right arcs with equal radii and a straight segment between them, mutually tangent to the two arcs, representing the roll maneuver. Fig. 3 illustrates a typical result.
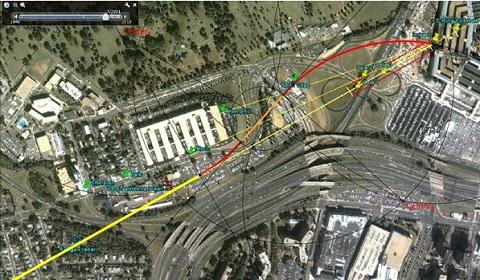
Figure 3: Path along the FDR route with turnoff level with Morin, 1 second roll time. The FDR track is shown in yellow, the left and right banks in red and the roll time in orange.
For a turn-off point level with Morin, with a 1 second roll time the results are:
|
Speed (mi/hr) |
Bank Angle (deg) |
g-Force |
|
552 |
85.3 |
12.1 |
|
530 |
84.8 |
11.0 |
The design limit for a Boeing 757 is 2.5g. Even if the plane somehow held together, it would be impossible to control during such an extreme maneuver.
If we reduce the roll time to (a clearly fictitious) one half second the values improve somewhat, but not enough to bring them within the range of plausibility:
|
Speed (mi/hr) |
Bank Angle (deg) |
g-Force |
|
552 |
84.7 |
10.7 |
|
530 |
84.2 |
9.9 |
Note that this scenario already conflicts with the testimony of Morin who stated that he watched the plane fly a considerable distance and descend behind a row of trees, with only the tall tail fin eventually being visible. It can be seen from the diagram (Fig. 3) that the plane would pass too quickly out of his line of sight. Note also that in this case the plane would disappear left wing first, his view obstructed by the vertical wall of the Annex, whereas we recall that he describes the plane disappearing from the bottom up, so his view must have been obstructed horizontally by the trees. We also see that witnesses would have seen the plane change from a steep left bank to a steep right bank between the Annex and the Citgo service station, but no such maneuver was reported.
If we now discount Morin’s description of the path of the plane entirely, and allow that he did not see it at all after it passed him, we can construct a scenario more favorable to the NOC hypothesis by moving the turn-off point earlier (Fig. 4). The last radar position provides the earliest point that the turn can reasonably be commenced. Morin’s observation that the plane flew nearly overhead is found to be preserved. Note that the curves are gentler.
Results, with a presumed 1 second roll interval:
|
Speed (mi/hr) |
Bank Angle (deg) |
g-Force |
|
552 |
77.9 |
4.8 |
|
530 |
76.9 |
4.4 |
With a half second roll interval we have:
|
Speed (mi/hr) |
Bank Angle (deg) |
g-Force |
|
552 |
77.5 |
4.6 |
|
530 |
76.5 |
4.3 |
This scenario, which totally disregards the testimony of Morin regarding the path of the plane (and there appears to be no justification for doing so) shows a substantially reduced g-force. It is still so high, however, that only someone with the skills of a trained fighter pilot would have a chance of performing it. The bank angle is still extremely steep.
The extraordinary bank angle
Anlauf and Paik would have seen the plane in a steep left bank and Morin would have seen it in a steep right bank. Hemphill would have seen the plane crossing from right to left of his line of sight to the impact point, at a steep right bank, as he looked out of his office window (Figs. 3 and 4 show his vantage point). These people reported no such thing. Hemphill repeatedly asserted that the plane was on his right and flying straight, and therefore with no significant bank. In the FDR file the maximum bank briefly recorded during this period was just 6°.
For these scenarios to work, the plane, after the roll, must maintain the steep right bank all the way to the Pentagon if it is to reach its target, which means the fuselage would have had to clear the roof of the Pentagon by nearly a wing-length, further straining the credibility of the “magic show” hypothesis.
The bank angle in all of these runs is so far out of the range of normal that, if it had happened, it would have astonished all observers. It would have been widely reported, yet nobody reported more than a slight bank. Albert Hemphill described the plane so close to the ground that he speculated about ground effect, which is clearly inconsistent with any of the calculated bank angles. Several of the witnesses indicated that the plane was flying “flat” in the vicinity of the Navy Annex, hence flying straight.[36] This is totally at odds with the necessary curve and bank angle.
CIT has provided assistance here, handing some witnesses a model plane so that they could illustrate the bank. The bank they show is slight. In particular we note that not one of the 13 witnesses, who claimed they saw the plane well enough to believe that it was NOC, mentioned that it was extremely steeply banked. The bank angle would have been glaringly obvious and, because of its strangeness, unforgettable.
Notes on the Calculations
The images used for these constructions are from Google Earth, with the history rolled back to September 12, 2001, (or September 13 for those of us west of the International Date Line). Note that, due to the camera location for this particular photograph, the roofs of the buildings are displaced a little south east relative to the footprints at ground level. The undulation of the landscape can induce similar small displacements. Positions relative to the footprints of buildings were used to avoid the former effect, and care was taken to centralize the point of interest in the screen, while placing markers, to minimize the latter. Since Geogebra is free, open source software, the reader can easily confirm this work and try other variations. We would like to thank the authors of Geogebra for the wonderful tool they have made freely available to the public.
The construction we used produces two arcs of equal radius separated by a stated interval along a mutual tangent (the roll interval), with one arc tangent to the path of approach and the other passing through a way point and the target. Deriving the construction is left as an interesting exercise for the reader.









We know that there is only one big story of 9/11, which the United States government presented and most of the people around the world accepted it as true. However, there were some who had some minor reservations about the details but they accepted the main account. Noam Chomsky happens to be one of them.
But what does the truth movement about the 9/11 say? A lot of experts, physicists, metallurgists, and engineers have offered their views that contradict the official version. Can some luminary explain why the opinions of these experts have been marginalised, ignored or not taken into account to look into the whole scenario of 9/11? There are far too many questions still in the air.
The following paper written by two experts throws some light on The Pentagon Attack on 9/11. Let’s hope among others Professor Chomsky will also find time to read it:
http://www.foreignpolicyjournal.com/2011/09/06/the-pentagon-attack-on-911/
There are many points to consider. Among them, men ponder that the fragile nose cone that hit the twin towers came through to the other side of the building without damaging the nose’s shape. The 10-foot ceilings on a 14 foot plane seems in consequential regardless of the chaos the sandwiching of it between floors naturally would have caused.
Masks at ready! Truth sets us free.
The nose cone would be the first thing to be completely pulverized. There is no evidence of a surviving nose cone. That is a red herring. Look at the Pentagon tab at http://www.911speakout.org and down at the bottom watch the crash test of a plane moving 500 mi/hr. That is a rough rendition of what to expect from the plane that hit the Pentagon. This is the approximate speed of the plane, so there would be the same amount of kinetic energy per unit mass, and the damage would be similar.
I want to say that I do not agree with terrorism, and I am just an Amateur Investigative Journalist who comments on matters following the Journalistic Code of Ethics of always being Honest, and of only stating genuinely held opinions.
England, France, and America are protected more than other Countries from revenge attacks that are labelled terrorism, especially given the fact that England France, and America are the Perpetrators of Evil Injustices on other innocent and defenceless Countries.
I read that the attack on the Pentagon on 11September 2001, could be only be done by American Elites, and that it was an unmanned American drone that hit the Pentagon.
The Video: The pentagon was not hit by an airliner, See for yourself, can be found on the internet at http://www.youtube.com/watch?v=FJR7OVJSdHs , unless the CIA changes the contents and location of that video in order to try to discredit me, and it does raise some very interesting questions.
There is an essential truth that needs to be made known, and that is that Satan and his demons want to have false stories that use only explanations that are natural in nature in order to Deceive People over true stories should give true explanations that are Supernatural explanations.
In other words, the Supernatural and true story of Creation, is explained by Secret Worshippers of the Invisible Demons using false stories of evolution that only give explanations that are natural in nature, but are lies.
It is the same with why England, France, and America have not been hit as hard with Terrorism as should be expected, because the Invisible Demons see everything that goes on in those Devil Worshipping Countries, and they torture in the invisible realm any Terrorists or revenge seekers to stop their activities or to be captured by looks like good Police and Intelligence gathering work (Mark 5:1-13).
England, France, and America are cunning, and so they allow some incidents that appear to be Terrorism to occur on their soil, like the London Bombing and September 11 thing, but these are manufactured by England, France, and America and blamed on Terrorists.
America had a foreign policy objective to invade and occupy Afghanistan and Iraq, and so they needed the excuse, and so they manufactured the excuse.
We, the Anglo-American Plutocrats are committed to Secret Devil Worshipping and to the Law of the Jungle, or Might is Right Rule.
The Politicians of England, France, and America asked the Invisible Demons to supernaturally torture Radovan Karadzic and General Ratko Mladic in the invisible realm until they surrendered, but it was made to look like naturally good Police Work.
America and the Modern Day Nazis of Europe are Secret Worshippers of the Invisible Devil and his Invisible demons, who are as real invisible and real as Gravity is, the Earth’s Magnetic Field, and Radio Waves.
Kosovo is a such a perfect example that nothing good can come from Devil Worship, because Devil Worshippers refused to love the truth and so be saved, they choose to delight in wickedness.
Illegally changing boundaries, or pressuring nations to change their borders is Devil worship, and that is why all decent people are opposed to it.
“You shall not murder. You shall not commit adultery. You shall not steal. You shall not give false testimony against your neighbour. You shall not covet your neighbour’s house. You shall not covet your neighbour’s wife, or his manservant or maidservant, his ox or donkey, or anything that belongs to your neighbour” (Exodus 20:13-17).
“Cursed is he who moves his neighbour’s boundary mark. And all the people shall say, Amen” (Deuteronomy 27:17).
“Do not move the ancient boundary which your fathers have set” (Proverbs 22:28).
If we read Acts 17:26-28 carefully, we will see that God wants people to worship Him in the boundaries of their country, and in a non-racist manner.
“And He made from one man every nation of mankind to live on all the face of the earth, having determined their appointed times and the boundaries of their habitation, that they would seek God, if perhaps they might grope for Him and find Him, though He is not far from each one of us; for in Him we live and move and exist, as even some of your own poets have said, For we also are His children” (Acts 17:26-28).
The true story of Kosovo is the true story of how the invisible Satan the Devil and his invisible demons have taken over the administration of America who controls the United Nations.
I know that people do not want to believe that such a thing can happen in Europe with the blessing of the United Nations, which is the main accomplice in this monstrous crime.
America wants to puppetize the Serbian people to steal their land and their resources.
We the people of Democracyland, whose national borders are defined by the United Nations Charter and International Law are committed to the highest form of democracy known to Mankind.
Democracyland will be a true democracy, by having no military alliances, by being 100% against racism, by having no genetically modified crops, by planting many trees, and by having 100% recycling.
We are left to wonder why FBI agents seized all videos from near-by places of business, and why they refuse to produce those videos, or any other evidence of a plane crashing into the Pentagon.
http://www.vaed.uscourts.gov/notablecases/moussaoui/exhibits/prosecution/P200022.html
Viewer discretion advised:
http://www.vaed.uscourts.gov/notablecases/moussaoui/exhibits/prosecution/P200042.html
http://www.vaed.uscourts.gov/notablecases/moussaoui/exhibits/prosecution/P200045.html
http://www.vaed.uscourts.gov/notablecases/moussaoui/exhibits/prosecution/P200047.html
http://www.vaed.uscourts.gov/notablecases/moussaoui/exhibits/prosecution/P200048.html
Plane or not, the big question is why the videos have not been released. The with-holding of that evidence should create suspicion in all skeptical and inquiring minds.
Indeed. It could be argued both ways. Some speculate they are withholding the evidence because it doesn’t show a plane hitting the Pentagon. I find this argument entirely unpersuasive (as this paper delves into), and there is no shortage of evidence that the plane hit the building. But one could also speculate that they are withholding the evidence precisely because permitting such speculation and “conspiracy theory” to persist helps to undermine the 9/11 truth community as a whole. The Toronto Hearings are an encouraging step forward:
http://torontohearings.org/
As an initial step I would suggest a common sense analysis of the available evidence from such sources as.
– The planes,where are what was left of them, the black boxes, or why they were not recovered. I gather evidence such as seating, passports? etc were recovered so there should be a wealth of evidence available which seems to be missing.
– The text-book collapse of the towers. In what circumstances is this possible?
– The time-line of the collapse of the towers including lead up and the collapse from beginning to end.
– The dust-cloud,its composition, quantity etc. Were samples taken? Where are they? What do they tell us?
After all this is where the proof is to be found.
Did the titanium alloy in the engines vaporize upon impact with the reinforced concrete walls? There aren’t obvious impact marks, although I’m not sure what would be the fate of titanium under such extreme conditions.
Honestly, though, the 9/11 movement is fragmented because it’s a theoretical guilty pleasure. Absence of evidence or full comprehension of the mechanics that led to WTC collapse or an unusual Pentagon impact zone for the claimed projectile are all inconsequential. Planes most certainly struck WTC, and although I’m curious to see the withheld Pentagon video evidence, I believe a plane struck the Pentagon, in accordance with the majority of eyewitness accounts. I didn’t always believe this as I allowed myself to be consumed with online CTs, and of course, the major independent internet documentaries produced on the subject. However, as I became more connected with the greater world, it started sounding more and more far-fetched. That’s because it is. Most 9/11 truthers, in my experience, are isolated in their own cliques (even in academia) and often do not participate in a substantial way in greater global society, as common 9/11 truth requires assuming unimaginable intentions and capabilities of an American organization. If 9/11 had truly been a coup, then it would look like a coup. It wasn’t enough to warrant martial law nor a profound expansion of emergency executive authority. Had it been a black op, as involved as rigging the WTC for collapse, it would’ve (successfully) included the Capitol building to ensure unprecedented powers for the American government and military during a complete crisis of government.
WTC did not collapse due to demolition. After the core steel was weakened and compromised, the downward acceleration of the in-tact upper floors into the lower floors beneath the impact zone would most certainly cause the runaway structural failure observed. I know this because it did. We all watched it on TV. It’s the same reason an entire deck of cards collapses simply because the top row does: the impulse from the falling part of the structure, accelerated by gravity and exerting a greater downward force than was ever intended or anticipated in the structural design, would clearly cause such a failure. It’s a simple explanation which is observed repeatedly in nature and is the only explanation which doesn’t require accepting something as fantastical and improbable as all 3 collapsed WTC towers were rigged for demolition. I no longer see the purpose of fabricating elaborate stories several orders of magnitude less likely than the commonly understood event, and suggesting extremely nefarious internal plots in the process. Citing the observed jets blasting away from the building during the implosion is the same fantastical approach to the available data (grainy videos). Knowing the elevator shafts in the buildings were hermetically sealed, extreme pockets of pressure were certainly created during the downward accordion-like compression. Such high pressure fissures would be expected to be present when considering the topography of the building in a collapse event; the secretly planned demolition of the two tallest structures in America, however, (and Building 7 for some undoubtedly extremely elaborate purpose) just sounds like 9/11 wasn’t mentally stimulating enough for certain people as it was.
I made up stories along with everyone else in disconnected online pockets, each picking and choosing which event was a cruise missile, which was hijacked airplanes, etc, but all it served was the exact same purpose 9/11 served: to delude people into believing an extreme about our government, whether one of willful international retribution or an Orwellian state which fabricates a foreign policy in order to pursue a material foreign policy. Both are misleading and contribute to polarized views of policy: some being there are no such things as terrorists (as every terror event is false flag), the rest that we have an inherent right to pursue non-descript enemies into whatever country we are led. Neither serve us, as one avoids an unfortunate contemporary danger, the other is the breeding ground of said contemporary danger.
Osama bin Laden is (was) a real guy. A Navy team killed him. He really did finance and direct an extremist group. He crossed common paths for common interests with the US in the past, much like Nazi Germany and Soviet Russia did. But after the Gulf War and the installation of US military bases in the Saudi Peninsula, extremely unpopular in Arabia, the stage was set for a retooling of his organization after the fall of Communist Afghanistan to direct his efforts against the occupation of Arabia and Palestine.
It makes perfect sense, the main official story. It’s the truth about 9/11. There is rich geopolitical history leading up to the tensions which eventually boiled over in the latest of a string of terror attacks perpetrated by a well-known and well-born fanatic. Maybe Flight 93 was shot down over Shanksville; there may be variations between the official account and reality, but the pith is the historical truth.
The government ‘knew’ there would be more attacks by al Qaeda after the US Embassy bombings in Kenya and the USS Cole. You can choose to believe the highest intelligence circles were aware of the attacks, or that particular government structures were altered to favor incompetence in the face of aviation crises (such as Norad being placed under the command of Dick Cheney), but to what extent of this is true and what’s coincidence is also inconsequential. The US has no desire to adjust its foreign policy which have guaranteed full access to the most convenient form of energy on Earth. Preventing an attack would not allow the US to mobilize into key resource bearing states with a permanent presence, so again, whether or not our intelligence community was aware is inconsequential, as the attacks were going to occur with or without prior knowledge, allowed to happen as it was a contained catalyst, or simply an event no one bothered predicting as, again, it was in the interest of our greater foreign policy for it to occur. Since the top layer, the New American Century layer wanted it to occur, there would be no need to direct intelligence toward islamic terrorist threats.
The truth is the very issue being avoided as straw men are chased: the US has an energy problem. We have allowed oil men, in the wake of an unimaginable tragedy caused by a sinister retaliation to our subjugation of middle eastern peoples, to ironically throw our entire nation’s economy into a new war effort, with taxpayer dollars flowing into Dick Cheney’s companies. But really, what else would you expect from a capitalist Vice President overseeing an administration attacked by the very people sitting on the oceans of gold he wants to extract? The problem is not Dick Cheney; we should expect crooked men like that to abuse their power. He probably intended to oversee legislation to promote favorable business conditions for him, yet his fate gave him access to more than he could’ve imagined. He actually would get to participate in the New American Century at government’s top tier, a philosophy who’s value has been quickly measured as we come to terms with the New Chinese Century.
American Intelligence, at whatever layer or allegiance, did not perpetrate 9/11. It took 10 years for me to fully accept this. I now feel shamed for the wasted time, but it has allowed me to consider our honest situation as a nation: the planet’s finite energy resources are rapidly coming into contention much sooner than anticipated due to the rise of Asia. Our dinosaur oil men leaders during 9/11 decided the way to deal with expected religious blow back from our national energy policy (huge amounts of wealth being exchanged with the gulf region) was to invade and install permanent military bases in two sovereign nations, one being possibly the most islamicized government on Earth, the other being a predominantly ethnic Arab country, unrelated to the terrorism that brought us but directly related to the energy we came for. Before 9/11, only extremists carried such an unfavorable view that they would sacrifice their lives in the name of Islam against the US. Now, we have secular Iraqis, who’ve lost wives or children, who wish revenge on us, and rightly so I might add.
9/11 conspiracy theories and 9/11 reactionarianism have completely missed the soon-to-be crisis that this tension is ultimately about: a finite and rapidly depleting resource. I’ve been saying this every 9/11, but a decade later and with the troop numbers diminishing in the middle east, I feel it’s more important than ever to remind Americans that we should not and should not ever have bound ourselves and our economy and industry to energy resources from outside our country. I’ve heard it said that America has a policy of consuming the greater world’s resources before our own, but we don’t need it anyway. We don’t need Saudi Arabia. Our soldiers don’t belong in a desert outpost indefinitely. The middle east has suffered oppression, tyranny, and 3rd world conditions in many parts, despite the fabulous natural resources, due to the West’s historical suzerainty and recent political influence and installments, in order to exclude as much national gain from the people of the host country as possible from the oil exports, maximizing US corporate profits. It was only a matter of time before our affairs reached our doorstep.
Energy research. There truly are exciting new technologies on the horizon. Imagine if we chose not to go to war after 9/11, withdrew all troops from the Arab World, and instead invested the 1 trillion dollar war tab paid to the profiteers into fusion research, a state of the art energy distribution system to support electric vehicles, research into the mass fabrication and commercialization of breakthrough low energy absorption / high-energy transmission ultra-efficient semiconductors such as Gallium Nitride based substrates to dramatically reduce transmission/energy losses, investment into additional grid power plants to support the addition of electric vehicle demand, and even massive research undertakings of similar scope to the Manhattan Project or the Apollo missions, by beginning to experiment methodologies with which to export solar energy from outside of our atmosphere in a massive scale to the surface for consumption. It sounds like science fiction to those who reacted to 9/11 as a need to further involve ourselves in the middle east; to much us, though, it’s an approaching reality which will be dealt with in our lifetimes, preferably on our terms.
We can do this. It needs to start with having a mature, forward thinking, undistorted view of how our internal crises or shortcomings are manifested in foreign policy, be honest with ourselves as to its cause, and rid ourselves from the countdown to total war the oil dependent world is slowly marching toward. Dick Cheney won’t be alive for it; I will be. Please help me make sure we’re comfortably watching it from the sidelines.
Peace on 9/11…
TO JC, who posted on 9/11/11:
Your post began promisingly, but ended as though written by a member of the Bush cabal. You cannot possibly produce the science that allows for the total collapse of the WTCs in their own footprints in near free-fall acceleration, after small fires in contained areas, of less than two hours duration. David Chandler, one of the authors of the article on the Pentagon to which you are responding, has written and spoken extensively on the impossibility of the buildings collapsing as described by FEMA and the 9/11 Commission Report.
Your logic seems to be that “it must have happened that way because we saw them ‘collapse’, and therefore it happened, just the way were were told by the authorities” without any critical thinking whatsoever. And what of WTC 7, the building that was not hit by any plane, yet collapsed in a perfect controlled demolition at 5:20 p.m. that same day. David Chandler has demonstrated that this building accelerated at free-fall speed for over 2 seconds. That is impossible without explosives being used to destroy the structure.
While your comments about depleted energy are relevant and important, you have completely missed the boat on the bigger topic of 9/11. To say that it was not a black ops or coup because the government was not destroyed entirely and Marshall law was not declared is facile; the Patriot Act eviscerated our civil rights, three wars have been fought in the name of the endless “war on terror”, millions have died for no reason, the Bush cabal was illegally elected twice through vote rigging and Supreme Court shenanigans, our Treasury has been depleted while the corporate powers have been enriched beyond their wildest expectations.
“It makes perfect sense, the main official story. It’s the truth about 9/11.”
I can’t help but get the impression that your expressed views as exemplified by the statement above are designed to distract people from the real truth about what happened that day. It cannot possibly have been that the main official story was in any way true; that has been shown over and over again by many reputable scientists and investigators, from Richard Gage to David Ray Griffin. It is too bad that you have chosen the path of dishonesty and distraction, when it seemed that you at one time had some real insight.
Other statements included in your analysis are patently wrong. You failed to mention that Osama Bin Laden was a CIA asset. And how are you so sure he died recently, when no photos have been released (Pentagon redux?), and the story of his alleged demise has changed many times.
I am extremely disheartened by the distortion of known events in your post.
(Noam Chomsky happens to be one of them.)
Chomsky spread the US government lies about 9/11 to protect the zionist tribe’s interest.
No one trusts Chomsky and his ilks ‘democracy Now’. Everyone believes this gang spread US goverent rubbish to fool people.
http://www.globalresearch.ca/index.php?context=va&aid=26948
Chomsky who presents himself as “anti imperialism’ accepted US government’s lies on 9/11 which was an inside job to protect the interest of Israel and her supporters the United States elite.
Chomsky also supported the war in Libya, quitely, and in print confess that NO FLY ZONE CAN BE JUSTIFIED. Don’t trust the pseudo ‘left’, which in fact spread the lies of the US imperialism/zionism.
TO JC, who posted on 9/11/11:
Your post began promisingly, but ended as though written by a member of the Bush cabal. You cannot possibly produce the science that allows for the total collapse of the WTCs in their own footprints in near free-fall acceleration, after small fires in contained areas, of less than two hours duration. David Chandler, one of the authors of the article on the Pentagon to which you are responding, has written and spoken extensively on the impossibility of the buildings collapsing as described by FEMA and the 9/11 Commission Report.
Your logic seems to be that “it must have happened that way because we saw them ‘collapse’, and therefore it happened, just the way were were told by the authorities” without any critical thinking whatsoever. And what of WTC 7, the building that was not hit by any plane, yet collapsed in a perfect controlled demolition at 5:20 p.m. that same day. David Chandler has demonstrated that this building accelerated at free-fall speed for over 2 seconds. That is impossible without explosives being used to destroy the structure.
While your comments about depleted energy are relevant and important, you have completely missed the boat on the bigger topic of 9/11. To say that it was not a black ops or coup because the government was not destroyed entirely and Marshall law was not declared is facile; the Patriot Act eviscerated our civil rights, three wars have been fought in the name of the endless “war on terror”, millions have died for no reason, the Bush cabal was illegally elected twice through vote rigging and Supreme Court shenanigans, our Treasury has been depleted while the corporate powers have been enriched beyond their wildest expectations.
“It makes perfect sense, the main official story. It’s the truth about 9/11.”
I can’t help but get the impression that your expressed views as exemplified by the statement above are designed to distract people from the real truth about what happened that day. It cannot possibly have been that the main official story was in any way true; that has been shown over and over again by many reputable scientists and investigators, from Richard Gage to David Ray Griffin. It is too bad that you have chosen the path of dishonesty and distraction, when it seemed that you at one time had some real insight.
Other statements included in your analysis are patently wrong. You failed to mention that Osama Bin Laden was a CIA asset. And how are you so sure he died recently, when no photos have been released (Pentagon redux?), and the story of his alleged demise has changed many times.
I am extremely disheartened by the distortion of known events in your post.
nikogriego – I agree. JC’s post was misleading.
J.C: “It makes perfect sense, the main official story. It’s the truth about 9/11.”
The WMD story put about by Bush and Blair and Powell also made “perfect sense” and was “the truth” until it all turned out to be a fabricated lie.
The “Anthrax Posted by Evil Arabs” made perfect sense and was punted as “the truth” until it turned out the Anthrax was made in a secure US lab and was posted by Americans, killing other Americans. ie. Arabs had nothing to do with it.
The “Evil Ones Pulled Babies Our of Incubators and Left Them to Die” story punted by a young girl in the US Congress, swinging the vote for Bush Snr’s first Gulf War, seemed to make “perfect sense” and be “the truth” until it was proven to be a press release drafted by Hill & Knowlton PR agency and read out by one of the Bush crony-Arab dictator’s young female relatives.